Análise Exploratória de Dados: do zero ao insight

A análise exploratória de dados é um dos corações de quem trabalha na área, pois é justamente o momento de você conhecer o seu objeto de estudo. Neste post vou discutir ideias dessa prática.

A análise exploratória consiste em:

• procedimentos para analisar dados

• técnicas para interpretar resultados

• caminhos de planejamento da reunião de dados para tornar a análise mais fácil

• toda maquinaria e resultados estatísticos aplicáveis à análise de dados

Probabilidade vs. Estatística

Primeiramente, vamos diferenciar esses dois conceitos importantes para o entendimento da prática. Basicamente, existe na natureza um processo gerador de dados que depende de certos fatores.

A probabilidade avalia o processo gerador para os dados observados. Então, a partir de informações sobre seu processo gerador será calculado a probabilidade de algo ser observado. Existem processos geradores na teoria que são conhecidos como distribuição de probabilidade, por exemplo, distribuição normal (Não será o foco do post). Enquanto isso, a estatística avalia o caminho dos dados observados para o processo gerador de dados, ou seja, a partir de dados observados, consigo concluir informações sobre o processo de geração.

Tipos de dados

• Dados quantitativos: são numéricos e mensuráveis, usados para contar ou medir (ex: número de clientes, idade). Eles podem ser contínuos ou discretos.

  • Contínuo (ex: salário, massa)

  • Discreto (ex: idade, número de filhos)

    
    

• Dados qualitativos: são descritivos e não numéricos, utilizados para entender percepções e experiências (ex: opinião, satisfação, sexo). Eles podem ser nominais ou ordinais.

  • Ordinal: dá para ordenar (ex: classe social, nível de satisfação)

  • Nominal: não dá para ordenar (ex: gênero, estado civil)

Processo de uma análise exploratória

1. Dados coletados

2. Tipos de dado

3. Como meus dados se parecem?

   • Usar gráficos.

   • Explorar ligações e interações.

4. Há algo de estranho nos meus dados?

   • Momento de limpeza dos dados.

   • Verificar outliers, erros, informações extremas e informações perdidas.

5. De qual fórmula esse dado veio?

   • Analisar distribuições de probabilidade.

   • Realizar transformações.

6. Quais testes podem ser realizados?

   • Exemplo: Regressão linear, chi-quadrado de Pearson, Testes de normalidade etc.

Gráficos e Sumários numéricos

Os gráficos são extremamente importantes para revelar informações ocultas e ter noção de como os dados estão distribuídos.

Os sumários numéricos são importantes, pois fornecem um resumo maior do que está contido nos gráficos e é uma informação que permite fazer cálculos. Alguns sumários numéricos são: Medidas de centralidade, dispersão e assimetria. Vamos avaliar alguns:

Medidas de centralidade

Descrevem “onde” os dados se concentram

1. Média: Trata-se de um ponto, onde posso resumir informações.

   • Existem muitas pessoas que focam muito em estudar os dados olhando apenas pela média, mas isso é extremamente perigoso! Um dos grandes problemas é a sensibilidade a outliers.

     • Ex: Suponha duas empresas. Na empresa A 9 pessoas ganham R$ 2.000 e 1 pessoa ganha R$ 50.000 e na empresa B 10 pessoas ganham R$ 6.000. Note que a média da empresa A é R$ 6.800,00 e da empresa B é R$ 6.000,00. Por qual delas você gostaria de ser contratado?

2. Mediana: Realização que ocupa a posição central na série de observações quando ordenada de modo crescente. Para calcular a mediana, ordene os dados e caso o número de dados seja ímpar, tome o valor central, mas caso seja par, tome a média dos dois centrais.

3. Moda: Observação mais frequente.

   • Em casos contínuos, onde, em geral, nenhum valor é repetido, é bom fazer uma análise de distribuição e não utilizar moda.

Medidas de dispersão

Medem o quão espalhados estão (variância, desvio padrão, amplitude, IQR). A variância e o desvio padrão medem variabilidade média em torno da média; quanto maiores, mais “espalhados” os dados.

Medidas de assimetria

Primeiramente, vou explicar o que é um quantil empírico: Um quantil de ordem p (ou p-quantil), denotado por q(p) com 0 < p < 1, é o valor tal que 100.p % dos dados estejam abaixo de q(p).

Os quartis mais famosos são o primeiro quartil (Q1) que é a mediana da metade inferior e o terceiro quartil (Q3) que é a mediana da metade superior, além disso o segundo quartil é a mediana. Basicamente, Q1, Q2 (mediana), Q3 indicam posições na distribuição (25%, 50%, 75%), ou seja, se Q1 = 9 significa que cerca de 25% dos dados possuem valores menores do que 9.

Por exemplo, dados (n=10): 2, 3, 4, 8, 10, 12, 15, 18, 21, 30

• Mediana = (10+12)/2 = 11

• Metade inf.: 2, 3, 4, 8, 10 → Q1 = 4

• Metade sup.: 12, 15, 18, 21, 30 → Q3 = 18

Dentro desse contexto, uma outra medida importante é a distância interquartil (IQR) = Q3 − Q1, a qual mede a “largura” do miolo (50% central), robusta a outliers (quando não há colapso por empates).

Gráfico Boxplot

É um gráfico para avaliara a dispersão dos dados usando os quartis. O gráfico é composto por uma caixa que indicará a proporção da quantidade de dados entre os 3 quartis.

• Vantagens: compacto, compara grupos bem.

• Limitações: com muitos empates (IQR=0) ou distribuições multimodais, pode ocultar estrutura; complemente com histograma/densidade/violin.

Como quantificar relações entre variáveis

Por fim, vou mostrar quais estatísticas mais recorrentes de serem usadas para relacionar variáveis de acordo com seu tipo. Aprenderemos medidas de correlação para ver o quanto associadas estão as variáveis. Depois vamos aferir estatisticamente se há de fato alguma associação.

1) Entre duas variáveis qualitativas

Buscaremos uma medida que retorne valor entre 0 e 1 (ou de -1 a 1). Nesse caso, valores próximos de zero indicam falta de associação. Primeiramente, devemos montar uma Tabela de Contingência (linhas = categorias de X; colunas = categorias de Y). É recomendado montar um mapa de calor ou mosaic plot para ver onde estão os desvios do “esperado”. Vamos ver algumas medidas:

a) Chi-Quadrada de Pearson

Diz se há alguma associação (p-valor), ou seja, iremos avaliar independência. Seja Oi valor observado e Ei o valor esperado de cada categoria, então temos a fórmula:

O problema da Chi-quadrada está apenas somando não levando em consideração o tamanho da tabela, assim quanto mais linhas maior será esse valor.

b) Coeficiente de contingência

O coeficiente de contingência de Pearson (C) quantifica a força da associação entre duas variáveis qualitativas (categóricas) a partir da tabela de contingência. Ele usa a chi-quadrada do teste de independência para n observações:

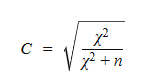
Note que C está entre 0 e um valor Cmax. Para tabelas retangulares r x c, o máximo é menor; uma boa regra prática é usar k = min{r,c} como referência para esse limite. Assim, obtemos o Cmax pela fórmula abaixo:

Como Cmax muda com o tamanho da tabela, C não é ideal para comparar associações entre tabelas de tamanhos diferentes. As vezes, será mais adequado normalizar o C por Cmax: C* = C/Cmax

2) Entre duas variáveis quantitativas

Um modo inicial é fazer um gráfico de dispersão, como scatter plot, entre duas variáveis. Procure padrão linear, curvilíneo, outliers ou grupos. Vamos introduzir medidas para verificar isso:

a) Covariância empírica

Procura indicar tendência de crescimento ou decrescimento entre variáveis.

Um problema dessa medida é quando temos variáveis em diferentes escalas, pois pode haver interferência das unidades das variáveis. Para tirar o problema da dependência da unidade usamos a correlação.

b) Correlação de Pearson

Força/direção linear (−1 a +1), sendo simples e muito usada. Ela irá avaliar alguma relação linear entre as variáveis. Ela é dada pela covariância dividido pela raiz quadrada do desvio padrão das variáveis.

É MUITO IMPORTANTE destacar que variáveis bem correlatas não implica causalidade. Isso é um erro bem comum quando isso é visto pela primeira vez. Outra coisa importante é que nem toda correlação é significativa, ou seja, nem toda correlação te ensina algo.

c) Spearman (ρ)

Deixarei indicado uma visão geral, basicamente é correlação de postos (ordem). Capta relações monotônicas (não precisa ser reta) e é mais robusta a outliers.

d) Kendall (τ)

É baseada em pares concordantes/discordantes; ainda mais estável em amostras pequenas ou com muitos empates.

3) Entre variáveis quantitativas e qualitativas

Não abordarei profundamente nesse momento, mas indicarei algumas coisas para você olhar. Na questão gráfica, visualize com boxplots por grupo (ou violin/histogramas sobrepostos).

Algumas medidas e testes úteis, destaco:

• Diferença de médias (2 grupos) → t de Student; se distribuição problemática, Mann-Whitney.

• Vários grupos → ANOVA (ou Kruskal-Wallis).

• Força da relação (percentual de variação explicada por grupos): η² (eta-quadrado).

  
  

Considerações

Analisar dados é, no fundo, aprender a fazer boas perguntas. Se este guia ajudou você a olhar além da média e a construir argumentos mais sólidos, já valeu a pena. Agora é sua vez: pegue um conjunto de dados do seu dia a dia, teste uma visualização, calcule um resumo — e veja que histórias aparecem. Se quiser, compartilhe nos comentários o que descobriu. Espero que esse guia sirva de instrução para os seus passos iniciais na análise exploratória de dados. Vou deixar o link do meu GitHub, o qual estarei alimentando com alguns projetos de análises exploratórias. Boa exploração!