Modelo de Markowitz e CAPM: Como otimizar carteiras de investimento

Vamos aprender a técnica de de otimização de carteiras.

Pré-requisitos: Probabilidade, Álgebra Linear e Noções de Finanças Quantitativas

Introdução

Por que duas carteiras com os mesmos ativos podem ter destinos tão diferentes?

Imagine dois investidores que compram os mesmos papéis. Um dorme tranquilo; o outro vive sobressaltado. A diferença não está nos ativos em si, mas em como eles foram combinados. É aqui que entram a Bala de Markowitz — o mapa risco–retorno das carteiras — e o CAPM, que conecta risco sistemático e retorno esperado. Neste post, você vai ver como desenhar essa bala, onde fica a tal fronteira eficiente, e por que o CAPM diz que é o beta que manda na conta quando há ativo livre de risco.

Teoria da carteira de Markowitz (Modelo da Média-Variância)

O objetivo da teoria da carteira de Markowitz é alocar de forma ótima recursos financeiros entre diversos ativos de renda variável, ou seja, determinar a composição ótima de

uma carteira ou portfolio de ativos financeiros de renda variável. Basicamente, nosso objetivo é descobrir como alocar uma riqueza xo entre ativos de renda variável com retornos R1, R2, ..., Rn.

Vamos calcular o risco-retorno da seguinte carteira:

com θi não negativos e Σ θi = 1. Para melhorar a notação, com o objetivo de trabalhar com vetores, usaremos:

Ao plotar diferentes combinações de θ temos a chamada Bala de Markowitz. Nela existe uma região, a fronteira da bala em sua parte superior, onde estão as carteiras com melhor risco-retorno. Esta região é chamada de fronteira eficiente.

Bala de Markowitz para n = 3 (fig. Cabral[1])

Uma vez definida a formulação, existem dois tipos de problemas de otimização com restrição que envolve. Cada um deles dependem do seu interesse.

a) Problema 1: Fixe o risco máximo

A questão é: “Tenho um orçamento de risco. Dentro desse risco, qual a carteira mais rentável?”. Fixado o risco máximo σo, vamos encontrar a carteira mais rentável.

b) Problema 2: Fixe um retorno mínimo

A questão é: “Tenho uma meta de retorno. Qual a carteira com menor risco que entrega essa meta?”. Fixado o retorno mínimo, vamos encontrar a carteira mais rentável.

Não se engane, ambos traçam a mesma curva (a fronteira eficiente), só que você percorre a curva:

• no Problema 1 variando o limite de risco;

• no Problema 2 variando o alvo de retorno.

A fronteira eficiente é o conjunto de respostas ótimas conforme você varia o “orçamento de risco” (P1) ou a “meta de retorno” (P2).

Modelo CAPM (Capital Asset Pricing Model)

O cenário é semelhante ao abordado acima, mas incluiremos a renda fixa. A adição desse termo visa o desejo de qualquer investidor em renda variável que é o "retorno esperado acima daquele proporcionado pela renda fixa".

Nesse cenário, vamos trabalhar o CAPM usando o Índice Sharpe, o qual possui a ideia de entender quanto retorno temos por cada unidade de risco.

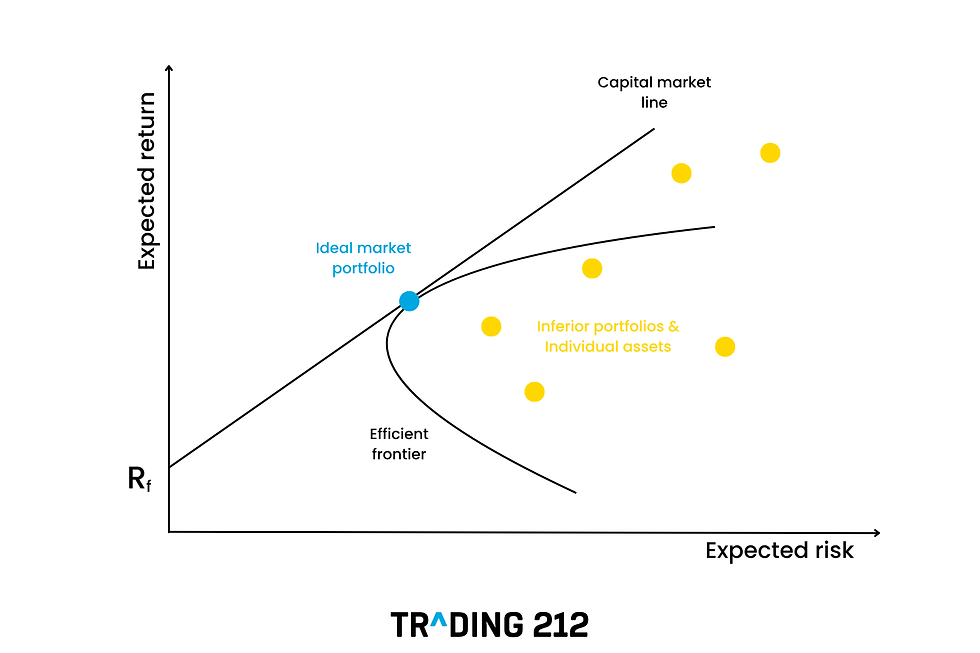
Em termos de finanças, estamos analisando o ativo livre de risco. Sem ele, a sua “Bala de Markowitz” (o mapa risco–retorno das carteiras só com ativos arriscados) é uma curva. Agora, com a adição da renda fixa haverá uma reta que começa em ro e tangencia a bala no ponto de maior Sharpe (a carteira tangente).

Essa reta é a Linha do Mercado de Capitais (CML).

Gráfico risco x retorno com CAPM (imagem retirada de Trading 212)

Em resumo

Vantagens e desvantagens

a) Markowitz

Vantagens

• Fundação conceitual clara: coloca o trade-off risco–retorno num problema convexo; com isso há soluções estáveis e “ótimas” sob os insumos.

  
  

• Interpretabilidade: risco como variância, retorno como média — fácil de explicar e visualizar (bala + fronteira eficiente).

  
  

• Soluções fechadas (sem restrições de sinal) e solvers padrão quando há restrições (QP).

  
  

• Baseline universal: ponto de partida para quase todo o resto (GMV, tangente, Black–Litterman, robusto, parity, etc.).

Desvantagens

• Normalidade / média–variância: trata risco como variância; ignora assimetria e caudas (penaliza upside e não captura risco de fila grossa).

  
  

• Covariância constante: supõe Σ fixa; na prática, covariâncias mudam no tempo (regimes, crises).

  
  

• Alto erro de estimação: μ e Σ são difíceis de estimar; pequenas variações viram grandes mudanças de pesos.

  
  

• Concentração extrema: soluções “puras” tendem a concentrar em poucos ativos (especialmente com μ ruidoso).

  
  

• Modelo estático de um período: ignora rebalanceamentos dinâmicos, custos/tributos, restrições reais (lotes, alavancagem limitada).

  
  

• Sensível a inputs: forecasts de retorno (difíceis) dominam a alocação; mudanças mínimas geram carteiras muito diferentes.

b) CAPM

Vantagens

• Regra simples de precificação​

  
  

• Interpretação clara: só o risco sistemático (beta) é remunerado.

  
  

• Separação em dois fundos: simplifica a decisão — um portfólio de risco (mercado/tangente) + renda fixa.

  
  

• Benchmark e linguagem comum: base para custo de capital, avaliação de performance (alfa/beta), comparação entre gestores.

Desvantagens (clássicas e empíricas)

• Hipóteses fortes: empréstimo/aplicação a rf sem fricções; expectativas homogêneas; um período; sem impostos/custos.

  
  

• Carteira de mercado não observável: “Roll’s critique”; na prática usa-se proxy (índices) com viés.

  
  

• Beta instável: β muda no tempo (mudanças estruturais/regimes), e seu poder explicativo não é total.

  
  

• Quebras empíricas: anomalias cross-section (tamanho, valor, momentum, qualidade) não são capturadas por um único fator.

  
  

• Mercados com fricções/restrições: alavancagem limitada, short proibido, custos e tributação afastam o equilíbrio do CAPM.

Técnicas de otimização/estimação de portfólio

O CAPM é um modelo de precificação em equilíbrio cujo objetivo é relacionar retorno esperado ao risco sistemático (beta) e, em equilíbrio, identificar a carteira de mercado. Existem também técnicas de construção/otimização de carteiras — eles escolhem pesos dados certos insumos (médias, covariâncias, restrições, custos, medida de risco) para obter pesos implementáveis. Vou listar alguns para o leitor (posso abordar alguns no futuro):

• Mean-variance com shrinkage

• CVaR

• HRP

• Black--Litterman

Há modos de conectar o CAPM com alguns deles, por exemplo, você pode usar o CAPM para estimar μ (prêmios esperados) e depois otimizar com um desses métodos (ex.: mean–variance com shrinkage em Σ e penalização de turnover). Os itens listados não “calculam o CAPM”. Na verdade eles melhoram a construção da carteira e mitigam fragilidades do Markowitz.

Implementação

Realizei algumas implementações desses modelos que pode ser encontradas no meu GitHub.

Conclusão

No fim das contas, a Bala de Markowitz e o CAPM seguem valiosos como bússolas conceituais: a primeira organiza o trade-off risco–retorno e mostra por que a diversificação importa; o segundo explica, com o ativo livre de risco, por que o beta do mercado é a régua de precificação em equilíbrio. Na prática, porém, estimativas imperfeitas (de retornos e covariâncias), mudanças de regime e fricções exigem variações modernas: covariâncias dinâmicas e com shrinkage, otimizações com regularização e custos, medidas de risco de cauda (CVaR/drawdown), estruturas como Risk Parity/HRP e modelos multifatoriais (Fama–French, momentum, qualidade). Usados assim — como baseline e ponto de partida para versões robustas — Markowitz e CAPM continuam sendo ferramentas centrais para transformar intuição em carteiras executáveis.

Referências

1. Livro Finanças Matemática Teoria e Prática - Marco A. P. Cabral

2. Trading 212 (capital-asset-pricing-model)

3. Markowitz, H. (1952). Portfolio Selection. Journal of Finance.

4. Sharpe, W. F. (1964). Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk. Journal of Finance.

5. GitHub com trabalhos/projetos de otimização de carteiras